Zastanawiasz dlaczego nowe struny brzmią inaczej niż te zużyte? Czy faktycznie warto wymienić je przed wejściem do studia lub większym gigiem?
Najbardziej interesująca część - eksperyment - jest poprzedzona masą teorii, więc jeżeli chcesz jedynie rzucić okiem, to zapraszam do ostatniej strony z wykresami.
Praca może również pomóc studentom broniącym się z fizyki, reżyserii, realizacji czy inżynierii dźwięku, protetyki słuchu lub po prostu akustyki.

Harmoniczne drgającej struny
- Wstęp............................................................................................................................................................................................. 3
- Część teoretyczna................................................................................................................................................................ 4
2.1 Instrumenty strunowe......................................................................................................................................... 4
2.2 Ruch Harmoniczny................................................................................................................................................... 5
2.3 Prędkość oraz przyspieszenie w ruchu harmonicznym......................................................... 6
2.4 Składanie ruchu harmonicznego................................................................................................................ 8
2.5 Ruch drgającej struny........................................................................................................................................ 10
2.6 Analiza widmowa dźwięku............................................................................................................................ 13
2.7 Barwa dźwięku......................................................................................................................................................... 15
2.8 Przetwornik elektroakustyczny................................................................................................................. 16
- Część eksperymentalna............................................................................................................................................. 23
3.1 Układ pomiarowy.................................................................................................................................................. 23
3.2 Wyniki pomiarów................................................................................................................................................... 24
- Wnioski..................................................................................................................................................................................... 29
- Literatura................................................................................................................................................................................ 31
1. Wstęp
Struna to podstawowy element instrumentów muzycznych zwanych chordofonami. Na ich brzmienie ma wpływ wiele czynników fizycznych. Muzycy często przed koncertem zakładają do swoich instrumentów nowe struny aby ich brzmienie było „świeże”. Zużyta struna brzmi inaczej niż nowa. Dzieje się to za sprawą zawartości harmonicznych w widmie dźwięku. Głównym zamierzeniem pracy jest przedstawienie różnic w składzie harmonicznych dwóch jednakowych strun, z których jedna jest zużyta. W tym celu posłużono się analizą Fourierowską pozwalającą w szybki sposób przedstawić widmo harmoniczne pobudzonej do drgań struny. Praca podzielona jest na dwa główne rozdziały. Pierwszy z nich opisuje teoretyczne aspekty ruchu harmonicznego i jego analizę oraz przedstawia zasadę działania przetwornika elektroakustycznego wykorzystanego podczas pomiarów. Do pełnego opisu badanego zagadnienia niezbędna jest także interpretacja muzyczna. Środowisko muzyczne posługuje się subiektywną oceną jakości dźwięku. Używa do tego terminologii, która została wyjaśniona w jednym z podrozdziałów. Druga część poświęcona jest eksperymentowi. Omówiono w niej metodę pomiarową oraz wyniki badań.
2. Część teoretyczna
2.1 Instrumenty strunowe
Instrumenty muzyczne, w których źródłem dźwięku są drgające struny nazywamy instrumentami strunowymi lub chordofonami. Ze względu na sposób artykulacji dźwięku dzielą się one na smyczkowe, szarpane i uderzeniowe. W instrumentach smyczkowych wykorzystuje się technikę pocierania włosia smyczka o strunę. Tarcie to można zwiększyć sztucznie przez użycie kalafonii. Prowadzony po strunie smyczek wyprowadza ją z pozycji równowagi. Sprężystość struny przewyższa siłę tarcia by następnie znowu poddać się działaniu smyczka i tak proces ten powtarza się. Najbardziej znanymi instrumentami smyczkowymi są skrzypce, altówka, wiolonczela i kontrabas. W przypadku szarpnięcia struny wytrąca się ją z pozycji równowagi za pomocą piórka lub opuszka palca. Jest to najstarszy znany sposób artykulacji. Dzisiaj najpopularniejszym instrumentem szarpanym jest gitara. Struna zachowuje się bardzo podobnie w instrumentach uderzeniowych, w których w drgania wprawia ją młoteczek lub pałeczka. Bardzo istotny jest także punkt, w którym pobudza się strunę do drgań. Tę ostatnią grupę chordofonów reprezentuje fortepian i pianino.
W starożytnej Europie nie praktykowano gry na instrumentach strunowych za pomocą smyczka. Technika ta nie była znana Rzymianom i Grekom. Rozpowszechnili oni jedynie instrumenty szarpane jak lira czy kitara. Instrumenty smyczkowe, na starym kontynencie, pojawiają się dopiero w średniowieczu. Ich pochodzenie zawdzięczamy kulturom pozaeuropejskim. W środowisku hinduskim znany był instrument wykonany z długiej i cienkiej trzciny bambusowej. Nosił on nazwę ravanastron. Posiadał on kilka strun, które pocierano smyczkiem, również wykonanym z trzciny bambusowej. Z innych części Azji wywodzi się podobny do niego instrument o nazwie ometria. Jego komora rezonansowa była wykonana z łupiny orzecha kokosowego. Ze środowiska arabskiego wywodzi się rebec. Ten instrument był najbardziej podobny do późniejszego typu europejskiego [1].
2.2 Ruch Harmoniczny
Ruch punktu materialnego, względem stanu równowagi, powtarzający się w regularnych odstępach czasu nazywamy ruchem okresowym. Jego najprostszą formą jest ruch harmoniczny, który określony jest wzorem [2]:
![]() (2.1)
(2.1)
gdzie:
x(t) – przemieszczenie ciała w chwili t
A – amplituda
ω – częstość kołowa
t – czas
– faza początkowa zależna od położenia ciała w chwili t = 0
Amplitudą drgań, przedstawioną na rysunku 1, nazywamy wartość bezwzględną maksymalnego wychylenia ciała [3].
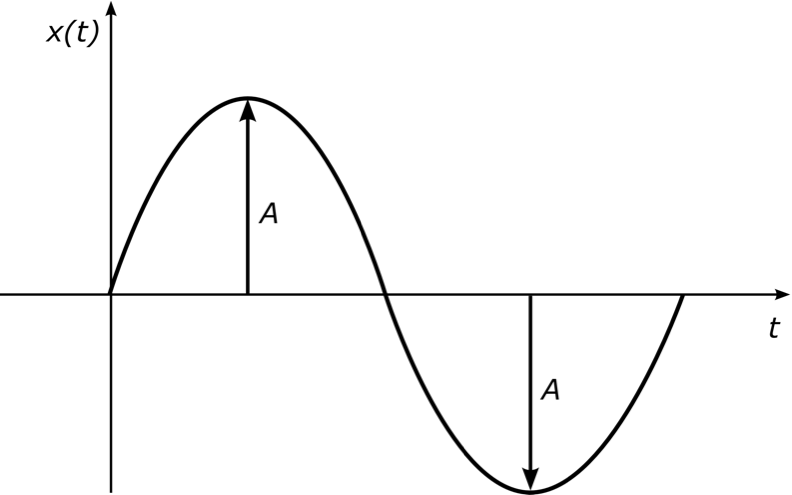
Rysunek 1 Zależność wychylenia punktu materialnego od czasu w ruchu harmonicznym.
Kolejnym parametrem fizycznym określającym ruch drgający jest częstość ν. W układzie SI wartość ta określona jest w hercach – Hz. Jest to liczba pełnych drgań wykonanych w czasie jednej sekundy. Wartością odwrotną częstotliwości jest okres T, czyli czas potrzebny do wykonania jednego pełnego drgania co pokazano poniżej [3].
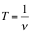 (2.2)
(2.2)
Rysunek 2. Ilustracja jednego okresu drgań w ruchu harmonicznym
Częstość kołowa wyrażana jest w radianach na sekundę i określana jest wzorem:
(2.3)
2.3 Prędkość oraz przyspieszenie w ruchu harmonicznym
Podczas ruchu drgającego zmienia się prędkość i przyspieszenie rozpatrywanego punktu materialnego. W przypadku prędkości, różniczkując równanie (2.1) po czasie otrzymujemy:
(2.4)
(2.5)
Podstawiając = otrzymujemy:
(2.6)
gdzie:
υ(t) – prędkość punktu materialnego w chwili t
- amplituda prędkości
Przyspieszenie punktu materialnego w ruchu harmonicznym obliczymy różniczkując równanie (2.5) po czasie:
(2.7)
(2.8)
gdzie:
- amplituda przyspieszenia
Położenie, prędkość oraz przyspieszenie w ruchu harmonicznym mają jednakowy okres T drgań. Wartość prędkości jest największa w momencie gdy wychylenie jest równe zeru i najmniejsza dla maksymalnego wychylenia. W przypadku przyspieszenia maksymalną wartość otrzymujemy przy maksymalnym wychyleniu. Przyspieszenie punktu materialnego jest zerowe w stanie równowagi [2].
2.4 Składanie ruchu harmonicznego
Punkt materialny może wykonywać kilka ruchów harmonicznych jednocześnie. Sumują się one zgodnie z zasadą superpozycji. Wypadkowy ruch składający się z n ruchów harmonicznych o tych samych częstotliwościach wyrażany jest wzorem:
(2.9)
gdzie:
A – amplituda, która jest określona wzorem:
(2.10)
Natomiast fazę początkową n drgających ruchów opisuje zależność
(2.11)
Przykład dwóch ruchów harmonicznych o tych samych częstotliwościach przedstawia rysuenk 3:
Rysunek 3 Ilustracja składania dwóch drgań harmonicznych.
Wypadkowy ruch złożony z n ruchów harmonicznych o różnych częstotliwościach wyrażamy wzorem:
(2.12)
Taki ruch nie jest ruchem harmonicznym i nie może być opisany równaniem (2.1). W szczególnych przypadkach ruch taki może być okresowy. Dzieje się tak gdy częstości drgań składowych dają się przedstawić wzorem:
(2.13)
gdzie:
i = 1,2,3,…,n
Podczas gdy częstości drgań składowych są niewspółmierne ale niewiele się od siebie różnią, powstają tzw. dudnienia. Zaobserwować można narastanie i zanikanie dźwięku. Efekt ten jest wyraźniejszy gdy amplitudy drgań są sobie równe.
Składanie ruchu harmonicznego może też odbywać się w dwóch prostopadłych kierunkach, gdzie:
, (2.14)
W tym przypadku torem, zakreślanym przez punkt materialny, jest krzywa stożkowa. Po wyrugowaniu czasu t otrzymujemy równanie na tor [4]:
(2.15)
Tor jest zależny od stosunku amplitud, częstości oraz różnicy faz. Przykładami takich torów są figury Lissajous przedstawione na rysunku 4:
a)
c)
b)
d)
Rysunek 4 Ilustracja figur Lissajous, w których częstotliwości drgań pozostają ze sobą w stosunku liczbowym a) 1:2, b) 1:2 z przesunięciem fazowym na osi x, c) 2:3, d) 3:4
2.5 Ruch drgającej struny
Struna jest cienkim, jednorodnym prętem, którego sztywność własną możemy zaniedbać wobec przyłożonego naprężenia. Jest ona układem jednowymiarowym i wykonuje drgania poprzeczne. Posiada nieskończenie wiele stopni swobody. Rozpatrując ruch drgający struny należy wziąć pod uwagę siłę naciągu Ts styczną do osi oraz gęstość liniową czyli masę przypadającą na jednostkę długości.
Drgania poprzeczne struny w stanie spoczynkowym są wyrażone wzorem:
(2.16)
gdzie:
w(x,t) – wychylenie poprzeczne struny
- prędkość fali poprzecznej w strunie
F(x,t) - siła wymuszająca na jednostkę długości struny
Gdy siła wymuszająca jest równa zeru otrzymujemy równanie drgań własnych struny:
(2.17)
gdzie:
f - częstotliwość drgań własnych struny
n = 1,2,3…
l - długość struny
Oprócz drgania struny na całej jej długości powstają również kolejne węzły dzielące strunę na 2,3,4 itd. Dalsze tony składowe to harmoniczne (alikwoty), a całe zjawisko nazywamy współtonem. Powstawanie harmonicznych drgającej struny nie zawsze musi być pełne. To samo dotyczy zanikania składowych harmonicznych podczas tłumienia drgania. Mówią o tym dwa prawa Younga. “Pierwsze Prawo Younga stwierdza, że struna nie może wykonywać takich drgań, w których węzeł przypada w punkcie pobudzenia struny” [1] tak jak to zostało pokazane na rysunku 5.
Rysunek 5 Tony składowe drgającej struny. ¯ - miejsce wzbudzenia drgań, w – węzły.
Zjawisko to jest bardzo często wykorzystywane przez muzyków chcących pozbyć się danej harmonicznej, która np. dysonuje z innymi dźwiękami.
Drugie Prawo Younga mówi o tym, że struna stłumiona sztucznie w jakimś punkcie wykonuje tylko takie drgania, których węzeł znajduje się w miejscu stłumienia. Zjawisko to wykorzystywane jest przez artystów do uzyskania tzw. flażoletu co pokazane jest na rysunku 6 [1,4,5].
Rysunek 6 Tony składowe tłumionej struny. ¯ - miejsce stłumienia drgań, w – węzły.
2.6 Analiza widmowa dźwięku
Podstawowym elementem analizy widmowej dźwięku niniejszej pracy jest analiza oparta na szeregu Fouriera. Pozwala on na rozkład harmoniczny funkcji opisującej drganie okresowe i wyraża się wzorem:
(2.36)
gdzie:
n – liczba całkowita większa od zera
Współczynniki ,, określone są następująco:
(2.37)
(2.38)
(2.39)
Szereg Fouriera przedstawia rozkład funkcji opisującej nieskończone drgania okresowe. W rzeczywistości jednak mamy do czynienia z drganiami skończonymi w czasie i są one z reguły nieperiodyczne. Analizę takich drgań można przeprowadzić za pomocą pary przekształceń Fouriera, które wyraża się wzorami:
(2.40)
(2.41)
gdzie odpowiednio równanie (2.40) – odwrotne przekształcenie Fouriera, (2.41) - Całka Fouriera [6]. Obecnie przekształcenia Fouriera wykonywane są za pomocą urządzeń cyfrowych takich jak cyfrowe oscyloskopy, analizatory widma i urządzenia audio. W praktyce najczęściej wykorzystywana jest dyskretna transformacja Fouriera DFT (ang. Discrete Fourier Transform). Algorytm taki oparty jest na sygnale próbkowanym, który jest przekształcany w dziedzinę częstotliwościową. Mając do dyspozycji pewną określoną liczbę próbek można obliczyć wartości amplitud oraz fazy harmonicznych badanego sygnału. Oprogramowanie wykorzystane w niniejszej pracy zbudowane jest w oparciu o ten algorytm [7].
2.7 Barwa dźwięku
Jedną z cech określających dźwięk jest jego barwa. To co dociera do słuchacza jako drganie złożone jest w istocie szeregiem drgań prostych o różnych amplitudach, częstościach i poziomach natężenia. W środowisku muzycznym do określenia barwy dźwięku używa się terminologii związanej z prostymi skojarzeniami i odczuciami. Brzmienie może być np. ciepłe, zimne, ciemne, jasne, okrągłe, ostre, nosowe, wyraziste, kwadratowe, płaskie. Fizyka posługuje się dokładniejszym opisem zjawisk akustycznych. Jest nim, wcześniej już wspomniana, analiza widmowa dźwięku. Czynność ta pozwala ściśle przebadać drgania złożone, a co za tym idzie – barwę dźwięku.
Powracając do praktyki muzycznej dźwięk dzieli się także na ton, współton, wieloton nieharmoniczny oraz szum. Ton jest dźwiękiem, którego wykresem jest sinusoida. Wydobycie takiego dźwięku z instrumentu muzycznego jest niemal niemożliwe. Jedynie w przypadku czelesty można uzyskać zbliżone brzmienie. Współtonem nazywa się wieloton harmoniczny złożony z pewnej ograniczonej liczby tonów składowych inaczej zwanych harmonicznymi lub alikwotami. Częstości tonów składowych są wielokrotnością tonu podstawowego tworząc szereg o stosunku liczbowym:
- ton składowy (podstawowy):200Hz
- ton składowy: 2x200Hz = 400Hz
- ton składowy: 3x200Hz = 600Hz
- ton składowy: 4x200Hz = 800Hz
itd.
Każdy ton składowy jest numerowany według swojego miejsca w szeregu bez względu na to czy występuje w danym drganiu. Nazwa oraz zapis nutowy pochodzi od pierwszego tonu składowego (tonu podstawowego), który określa jego częstość niezależnie od poziomu natężenia. Jest to spowodowane zdolnością ludzkiego ucha do odbierania współtonu jako jednego zjawiska. Wieloton nieharmoniczny jest także drganiem złożonym, pokrewnym współtonowi. Składa się on z ograniczonego szeregu harmonicznych lecz ich częstości nie pozostają ze sobą w określonym stosunku liczbowym. Przykładem takiego brzmienia są widełki strojowe, których dwie pierwsze harmoniczne drgają kolejno z częstościami 440 oraz 2758Hz. Innym przykładem może być trójkąt, którego widmo akustyczne nie przejawia żadnej regularności w odległościach pomiędzy harmonicznymi. Wieloton nieharmoniczny jest także odbierany przez ludzkie ucho jako spójne zjawisko jednak nie jest ono w stanie wyróżnić tonu podstawowego, a co za tym idzie – określić wysokości dźwięku. Można jedynie w przybliżeniu stwierdzić czy dźwięk jest wysoki czy niski, a zapis nutowy ogranicza się do zapisu rytmu oraz dynamiki. Ostatnim z czterech rodzajów dźwięku jest szum. Posiada on nieskończenie wiele tonów składowych, których częstości są do siebie bardzo zbliżone. Poza tym faktem definicja szumu jest taka sama jak w przypadku wielotonu nieharmonicznego. Wszystkie te zjawiska mogą występować jednocześnie. Podczas pocierania smyczkiem o strunę czy uderzania jej młoteczkiem występują zarówno wielotony jak i szum spowodowany mechaniczną artykulacją dźwięku (jako skutek uboczny) [1].
2.8 Przetwornik elektroakustyczny
Urządzenia, które zamieniają energię akustyczną na energię elektryczną lub odwrotnie nazywamy przetwornikami elektroakustycznymi. Najlepszym przykładem jest mikrofon i głośnik. W pracy wykorzystano przetwornik elektromagnetyczny, który działa w oparciu o elektromagnes. Przyciąga on kotwicę wykonaną z materiału ferromagnetycznego. Podczas gdy przez uzwojenie płynie prąd i, siła działająca na kotwicę wyrażona jest wzorem:
(2.18)
gdzie:
z – liczba zwojów elektromagnesu
S – powierzchnia przekroju rdzenia elektromagnesu
d – odległość kotwicy od rdzenia
- przenikalność magnetyczna powietrza
Koniecznym do liniowego przetwarzania sygnału jest zastosowanie stałego strumienia polaryzującego. Wykorzystuje się do tego magnes trwały tak jak na rysunku 8:
Rysunek 8 Konstrukcja jednobiegunowego przetwornika elektromagnetycznego
Gęstość energii pola magnetycznego w szczelinie powietrza wynosi:
(2.19)
gdzie:
w – gęstość energii pola magnetycznego
H – natężenie pola magnetycznego
B – indukcja pola magnetycznego
Jeśli szerokość szczeliny zmieni się o dx, zostanie wykonana praca:
(2.20)
gdzie:
- siła magnetyczna
Ze wzorów (2.19, 2.20) Otrzymujemy siłę magnetyczną:
(2.21)
gdzie:
- całkowity strumień magnetyczny
Strumień magnetyczny jest równy jeżeli przez uzwojenie elektromagnesu prąd nie płynie. Wytwarza on stałą składową siły, która powoduje przyciąganie kotwicy do nabiegunnika.
(2.22)
gdzie:
- stały strumień polaryzujący
W wyniku polaryzacji zmienia się szerokość szczeliny do wartości .
Wartość wyznaczamy z równania równowagi sił:
(2.23)
gdzie:
- mechaniczna podatność kotwicy
Wartość stałego strumienia polaryzującego zależy od szerokości szczeliny w następujący sposób:
(2.24)
gdzie:
M – siła magnetomotoryczna
Podczas polaryzacji magnesem trwałym siła magnetomotoryczna jest równa
(2.25)
gdzie:
- Natężenie pola magnetycznego magnesu trwałego
- długość magnesu
Jeżeli przez uzwojenie elektromagnesu płynie prąd zmienny i to strumień magnetyczny jest sumą stałego strumienia polaryzującego oraz zmiennego strumienia wytwarzanego przez prąd i. Jest on wyrażony wzorem:
(2.26)
gdzie:
x – wychylenie kotwicy zależne od prądu i
Siła działająca na kotwicę wyraża się wzorem:
(2.27)
Przy odpowiednich założeniach oraz rozwinięcia wyrażenia w szereg Taylora siła ta przyjmuje postać kilku składowych. Składowe nieliniowe powodują pojawienie się drugiej harmonicznej w pracy przetwornika. Aby przetwornik był efektywny należy dobrać odpowiednio dużą wartość stałego strumienia tak aby składowe liniowe stały się dominującymi. Po tych przekształceniach siła ta wyraża się wzorem:
(2.28)
następnie:
(2.29)
przyjmując oznaczenia:
(2.30)
(2.31)
wzór(2.29) można przedstawić w postaci:
(2.32)
Siła F na wyjściu przetwornika musi być pomniejszona o siłę potrzebną do poruszenia kotwicy. Kotwica jako rezonansowy układ drgający o parametrach: - masa czynna, - rezystancja mechaniczna, -podatność czynna, pozwala wyrazić impedancję jako:
(2.33)
Co następnie pozwala wyrazić siłę F na wyjściu przetwornika w postaci:
(2.34)
Aby przetwornik był stabilny musi być spełniony następujący warunek:
(2.35)
Schemat zastępczy przetwornika elektromagnetycznego przedstawia Rysunek 9 [5].
gdzie:
u – napięcie elektryczne na zaciskach uzwojenia
Re – rezystancja uzwojenia
Le – indukcyjność
i – natężenie
T1 – współczynnik przetwarzania elektromechanicznego
Ca – podatność
Cm – podatność czynna
Mm – masa czynna
Rm – rezystancja mechaniczna
F – siła na wyjściu przetwornika
3. Część eksperymentalna
3.1 Układ pomiarowy
W części eksperymentalnej zostało wykonane badanie harmonicznych drgającej struny za pomocą trzech doświadczeń. Do przeprowadzenia każdego z nich użyto lutniczej gitary elektrycznej. Instrument wyposażony został w przetwornik elektromagnetyczny DiMarzio D Sonic o napięciu wyjściowym 390 mV oraz impedancji 11,96 kΩ [8]. Następnie sygnał jest wzmacniany oraz przetwarzany z analogowego na cyfrowy za pomocą interfejsu audio Mbox AVID. Analiza widma odbyła się przy pomocy programu komputerowego Audacity z wbudowanym modułem FFT. Schemat układu pomiarowego przedstawiony jest na rysunku 10:
Rysunek 10 Schemat oraz fotografia układu eksperymentalnego.
Analizie zostały poddane dwie niklowane, ręcznie wykonane struny E1 firmy DR. Jedna z nich jest fabrycznie nowa, a druga zużyta tj. zniszczona na skutek długiego intensywnego używania.
W pierwszym doświadczeniu porównane zostały tony składowe(harmoniczne) tych dwóch drgających strun. Obie struny zostały zestrojone do częstotliwości 330 Hz(ton E1), a następnie pobudzane do drgań za pomocą piórka. Analiza widmowa tego zabiegu wyjaśnia różnicę w brzmieniu pomiędzy nową i starą struną. Dwa kolejne eksperymenty mają za zadanie zobrazować prawa Younga dotyczące zanikania harmonicznych. Do tych doświadczeń użyto tylko struny nowej. Różnica polega jedynie w artykulacji dźwięku. W pierwszym z nich struna została pobudzona do drgania dokładnie w połowie jej długości. Drugie Prawo Younga wymaga wydobycia flażoletu. Struna została sztucznie stłumiona opuszkiem palca w połowie jej długości, a następnie szarpnięta piórkiem. Czynność ta wymagała dużej precyzji i wielu prób.
Analiza widmowa drgań została przeprowadzona w granicach od 100 Hz do 20 kHz, a więc w zakresie częstotliwości słyszalnych przez człowieka.
3.2 Wyniki pomiarów
Wyniki eksperymentalne zostały zilustrowane na wykresach (1-3). Wykres 1 porównuje drgania struny starej (kolor niebieski) i nowej (kolor czerwony). Krzywa oznaczona kolorem zielonym to różnica w poziomie zarejestrowanego sygnału pomiędzy obiema drgającymi strunami. Wyniki pomiarów jasno wskazują na to, że poziomy sygnałów pierwszych sześciu harmonicznych są porównywalne. Pięciodecybelowa różnica pojawia się dla dziewiątej harmonicznej. Wraz ze wzrostem częstotliwości rozbieżności pomiędzy poziomami sygnałów poszczególnych harmonicznych są coraz większe. Największa różnica, wynosząca 19,6 dB, przypada dla częstotliwości 8957Hz. Z rysunku wyraźnie widać, że wyższe mody drgań struny nowej są zdecydowanie mocniejsze. W aspekcie psychofizycznym brzmienie jest jaśniejsze, pełniejsze i przyjemniejsze w odbiorze.
Kolejne dwa wykresy ilustrują pierwsze i drugie prawo Younga. Wykres 2 przedstawia zanik wszystkich parzystych harmonicznych, na skutek pobudzenia struny do drgań w połowie jej długości. Z pierwszego prawa wynika, że alikwoty, których węzeł przypada w miejscu wprawienia struny w drganie zostają zniwelowane. Szarpnięcie jej w połowie długości powoduje więc zanik co drugiej harmonicznej. Drugie prawo Younga stanowi odwrotność pierwszego. Z tego powodu na wykresie 3 można zaobserwować zanikanie wszystkich nieparzystych tonów składowych.
Próbki dźwiękowe zostały zapisane na płycie CD dołączonej do pracy. Plik 1.wav i 2.wav to dźwięki starej i nowej struny. Kolejne dwa pliki – 3.wav i 4.wav to dźwięki prezentujące odpowiednio I i II Prawo Younga.
Wykres 1 Widmo akustyczne drgających strun.
Wykres 2 Widmo akustyczne ilustrujące pierwsze prawo Younga.
Wykres 3 Widmo akustyczne ilustrujące drugie prawo Younga.
4. Wnioski
Bez wątpienia różnica w brzmieniu gitary, wyposażonej w nowy, a zużyty komplet strun jest znacząca. Dokładniejsze wnioski można wyciągnąć dopiero na podstawie analizy widmowej drgań. Kluczową rolę odgrywa poziom natężenia harmonicznych drgających strun. Nie przez przypadek pierwsza taka zauważalna różnica znajduje się w okolicach 2-4 kHz. Ten zakres częstotliwości to tzw. prezencja gitary. Jest ona odpowiedzialna za ogół brzmienia tego instrumentu. Jakakolwiek modyfikacja w tym paśmie powoduje natychmiastową zmianę charakteru barwy. Jest ona tym bardziej słyszalna ponieważ maksimum czułości ludzkiego ucha przypada na ten sam zakres częstotliwości. Krzywe izofoniczne ludzkiego ucha przedstawiono na rysunku poniżej.
Rysunek 11 Krzywe izofoniczne ludzkiego ucha [9]
Kolejna istotna różnica w poziomie natężenia alikwot znajduje się w przedziale powyżej 7 kHz. Dzieje się tak ponieważ nowa struna jest bardziej sprężysta i wolna od wszelkich zanieczyszczeń, dzięki temu drga w najwyższych częstotliwościach. W środowisku muzycznym, a zarazem aspekcie psychofizycznym, brzmienie jest jasne, wyraźne, przejrzyste. Często wydaje się być także przyjemniejsze i ciekawsze. Dźwięk nasycony najwyższymi tonami składowymi łatwiej przebije się przez grający zespół lub orkiestrę. Melodia jest bardziej zrozumiała i wydaje się być zagrana z większym impetem. Z szeregu tych powodów muzycy, udający się do studia nagraniowego, z reguły zaopatrują się w nowe komplety strun. Niekiedy jednak przesyt harmonicznych powoduje, że brzmienie z wyraźnego staje się za ostre. Przez wzgląd na to produkuje się również specjalnie oplecione struny imitujące brzmienie strun zużytych. Dzięki temu barwa z ostrej zmienia się w ciepłą ale nie traci swojej prezencji w przedziale 2-4 kHz tak jak to bywa przypadku faktycznie zużytych strun.
5. Literatura
- Drobner, Instrumentoznawstwo i akustika, PWM 1997
- Jaworski, Kurs fizyki tom 1, PWN 1971
- Halliday, Robert Resnick, Podstawy fizyki tom 2, PWN 2006
- Osiński, Teoria drgań, PWN 1980
- Dobrucki, Przetworniki elektroakustyczne, Wydawnictwa Naukowo-Techniczne 2007
- Ozimek, Dźwięk i jego percepcja, PWN 2002
- Baranowski , Mikrokontrolery AVR ATmega w praktyce, BTC 2005
- Nota katalogowa przetwornika D-Sonic 7™ Dimarzio 2003
- A. Everest, Podręcznik Akustyki, Wydawnictwo Sonia Draga 2013

